Die Prinzipien der speziellen Relativitätstheorie
Peter Schmüser

Die Spezielle Relativitätstheorie beeinflusst unseren modernen Alltag mehr als man denken mag. Navigationssysteme, Uhren und Partikel in riesigen Teilchenbeschleunigern gehorchen zum Beispiel ihren Prinzipien. Die Physik dahinter lässt sich auch ohne Mathematik nachvollziehen.
Ausgangspunkt der Speziellen Relativitätstheorie ist das Prinzip, dass die physikalischen Gesetze in allen Inertialsystemen dieselbe Gestalt haben. Unter einem Inertialsystem versteht man dabei ein System, das in Ruhe ist oder sich geradlinig und mit konstanter Geschwindigkeit bewegt. Einen guten Eindruck eines solchen Inertialsystems vermittelt ein Jumbo-Jet auf einem Transatlantikflug bei ruhigem Wetter und mit verdunkelten Fenstern. Wenn der Fluggast das Rauschen der Turbinen als Rauschen einer Klimaanlage deutet, wird er kaum unterscheiden können, ob das Flugzeug am Boden steht oder mit 900 Kilometern pro Stunde fliegt. Ein Passagier kann sich alle möglichen mechanischen, elektrischen oder optischen Versuche ausdenken, um die Geschwindigkeit des Jets zu messen. Es wird ihm nicht gelingen, solange diese Experimente auf den Innenbereich des geschlossenen „Kastens“ Flugzeug beschränkt bleiben und keine Signale von außen empfangen werden. Sobald aber das Flugzeug startet, eine Kurve fliegt oder landet, spürt man dies im Innern sofort. In diesen Fällen ist das Flugzeug ein beschleunigtes Bezugssystem, und dort gelten andere Gesetze als in einem Inertialsystem. Auch in einem Karussell oder einer startenden Weltraumrakete wird der Mitfahrer andere Gesetzmäßigkeiten feststellen. Solche beschleunigten Bezugssysteme sind Gegenstand der allgemeinen Relativitätstheorie.
Ein weiteres Beispiel für Inertialsysteme sind Rollsteige, die man zum Beispiel in vielen Flughäfen findet. Der Rollsteig und die ruhende Flughafenhalle bilden zwei Inertialsysteme, die sich relativ zueinander bewegen. Nehmen wir an, eine Frau auf dem Rollsteig hat es besonders eilig und läuft ihrem Ziel entgegen. Für einen Beobachter außerhalb des Transportbandes bewegt sie sich mit einem Tempo, das sich aus der Summe von Rollband- und Gehgeschwindigkeit ergibt. Würde die Reisende genauso schnell gehen wie der Rollsteig, nur in entgegengesetzter Richtung, so würde sie für einen außenstehenden Betrachter im wahrsten Sinne des Wortes auf der Stelle treten.
Diese einfache Addition oder Subtraktion der Geschwindigkeiten funktioniert im Alltag problemlos, doch sie hat Grenzen. Angenommen, die Frau bleibt stehen und macht mit ihrer Kamera eine Blitzlichtaufnahme in Vorwärtsrichtung. Danach dreht sie sich um und macht eine zweite Aufnahme in entgegengesetzter Richtung. Werden die beiden Lichtblitze von einem neben dem Rollsteig stehenden Beobachter ebenfalls als verschieden schnell wahrgenommen werden? Nach dem vorherigen Beispiel sollte das nach vorn fliegende Blitzlicht schließlich um die Geschwindigkeit des Rollsteigs schneller sein, das nach hinten fliegende entsprechend langsamer. Diese naive Betrachtungsweise erweist sich jedoch als falsch: Beide Lichtblitze sind genau gleich schnell.
Ein entsprechendes Experiment führten die beiden Wissenschaftler Albert Abraham Michelson und Edward Williams Morley Ende des 19. Jahrhunderts durch. Die beiden Forscher wollten feststellen, ob Lichtwellen genau wie Wasser- oder Schallwellen ein Medium brauchen, um sich auszubreiten. Dabei diente ihnen die Erde auf ihrer Bahn um die Sonne gewissermaßen als Raumschiff in einem hypothetischen Medium, das man „Äther“ nannte. Die große Überraschung war, dass Licht unabhängig von der Bewegungsrichtung der Erde relativ zu diesem Äther immer genau die gleiche Geschwindigkeit aufweist. Die Lichtgeschwindigkeit, meist abgekürzt mit dem Buchstaben c, ist also unabhängig vom Bezugssystem und beträgt im leeren Raum immer 299.792.458 Meter pro Sekunde – und zwar exakt.
Albert Einstein nahm die Konstanz der Lichtgeschwindigkeit zum Anlass, die Existenz einer absoluten und allgemein gültigen Zeit in Frage zu stellen. Er erkannte, dass die sogenannte Lorentztransformation den Sachverhalt richtig beschreibt. Die daraus folgenden relativistischen Formeln zur Addition von Geschwindigkeiten stellen sicher, dass die Lichtgeschwindigkeit in beliebigen Inertialsystemen stets 299.792.458 Meter pro Sekunde beträgt. Der wesentliche Unterschied zur einfachen Addition: Für gegeneinander bewegte Objekte gelten verschiedene Zeitskalen. Maßgeblich bestimmt werden diese durch den sogenannten Lorentzfaktor, der allein von der relativen Geschwindigkeit der Objekte abhängt.
Abschied von einer absoluten Zeit
Eine unmittelbare Konsequenz der Konstanz der Lichtgeschwindigkeit ist die Zeitdehnung oder Zeitdilatation: Vom Laborsystem aus betrachtet „tickt“ eine Uhr in einem bewegten Bezugssystem langsamer. Einstein verdeutlichte die Zeitdehnung durch eines seiner berühmten Gedankenexperimente: die Lichtuhr. Diese Uhr besteht aus einer Blitzlampe, einem Spiegel und einem Detektor. Die Blitzlampe sendet einen kurzen Lichtblitz in vertikaler Richtung aus, der zu einem Spiegel läuft, dort reflektiert wird und dann zum Detektor zurückläuft, wo sein Eintreffen durch ein Ticken angezeigt wird. Das Hin- und Zurücklaufen des Lichtblitzes entspricht dabei dem Hin- und Zurückschwingen des Pendels in einer Standuhr.
Bei der ruhenden Lichtuhr ist der Lichtweg durch den Abstand von der Lampe zum Spiegel und zurück zum Detektor gegeben. Bei der horizontal bewegten Lichtuhr bleibt der vertikale Abstand zum Spiegel unverändert, doch bis das Licht den Spiegel erreicht hat, ist der Spiegel bereits weitergeflogen, und bis das reflektierte Licht den Detektor erreicht, ist dieser noch weiter geflogen. Das Licht folgt also einer längeren Dreiecksbahn (siehe Grafik). Trifft man jetzt – Albert Einstein folgend – die fundamentale Annahme, dass das Licht in beiden Systemen exakt die gleiche Geschwindigkeit c besitzt, so benötigt der Lichtblitz, vom Labor aus betrachtet, mehr Zeit, um zum Detektor zu gelangen. Die Tickgeräusche ertönen also seltener, und der Zeittakt der bewegten Uhr erscheint dem ruhenden Beobachter verlängert, und zwar um den Lorentzfaktor. Bewegte Uhren gehen demnach langsamer. Die wichtigste Folgerung aus diesem Gedankenexperiments ist jedoch, dass in der Relativitätstheorie keine absolute Zeit mehr existiert. Das ist ein fundamentaler Bruch mit der Sichtweise der Naturwissenschaften und der Philosophie vor der Formulierung der Relativitätstheorie. Bis zum Ende des 19. Jahrhunderts ging man wie selbstverständlich davon aus, dass es eine absolute und überall gültige Zeit gäbe.
Da die Geschwindigkeiten von alltäglichen Körpern wie Flugzeugen oder Satelliten weit unterhalb der Lichtgeschwindigkeit liegen, ist die Verlangsamung bewegter Uhren hier äußerst gering. Mit hochpräzisen Atomuhren ist sie aber gut messbar und für das Globale Positionierungssystem GPS von großer Bedeutung. Bewegt sich der GPS-Satellit beispielsweise mit einer Geschwindigkeit von rund vier Kilometern pro Sekunde relativ zum Empfänger, würde die ermittelte GPS-Position ohne entsprechende Korrekturen schon nach zwölf Stunden um einen guten Kilometer neben der tatsächlichen Position liegen.
Elementarteilchen und Relativitätstheorie
Eine sehr wichtige Rolle spielt die Zeitdilatation für kurzlebige, massebehaftete und energiereiche Elementarteilchen, die zum Beispiel in Teilchenkollisionen erzeugt werden. Die Zahl solcher instabilen Teilchen nimmt exponentiell ab und ist nach der sogenannten Halbwertszeit auf die Hälfte abgesunken. Definiert ist diese Halbwertszeit für ruhende Teilchen, und das hat interessante Folgen: Bewegt sich ein Teilchen schnell durch das Laborsystem, misst ein Forscher darin eine um den Lorentzfaktor verlängerte Halbwertszeit.
Das bekannteste Beispiel sind die Myonen – schwere Verwandte der Elektronen – in der Höhenstrahlung. Erzeugt werden sie etwa zwanzig bis dreißig Kilometern über der Erde als Sekundärprodukte bei Stößen hochenergetischer Protonen aus dem Weltall mit Atomkernen der äußeren Lufthülle. Myonen zerfallen mit einer Halbwertszeit von rund 1,52 Mikrosekunden in ein Elektron und zwei Neutrinos. Innerhalb dieser kurzen Zeit könnten sie selbst mit Lichtgeschwindigkeit nur 457 Meter zurücklegen. Die Wahrscheinlichkeit, dass eines dieser Teilchen eine Strecke von zwanzig Kilometern „überlebt“, die immerhin 44 Halbwertszeiten entspricht, wäre verschwindend gering.
Doch Wissenschaftler beobachten, anders als eben abgeschätzt, dass zahlreiche Myonen der Höhenstrahlung den Erdboden erreichen. Die Lösung des Rätsels liegt in der Lebensdauerverlängerung durch die Zeitdilatation. Die Teilchen entstehen mit hoher Energie und damit hohen Geschwindigkeiten. Im Mittel verlängert sich ihre Halbwertszeit dadurch um das 16-fache, und die Flugstrecke, die die Hälfte der Myonen übersteht, beträgt 7310 Meter. Die Distanz von 20.000 Metern entspricht somit nur noch 2,7 Halbwertszeiten, und die Wahrscheinlichkeit, diese Strecke ohne Zerfall zurückzulegen, liegt nun bei 15 Prozent.
Wie sieht die Situation im Ruhesystem der bewegten Teilchen aus? Hier gibt es keine Halbwertszeitverlängerung, wohl aber eine Längenkontraktion. Dieses Phänomen ist eng mit der Zeitdilatation verknüpft: Ein bewegter Längenmaßstab wird von einem ruhenden Beobachter als verkürzt wahrgenommen, und zwar um den Lorentzfaktor. Aus Sicht der schnellen Myonen wirkt die 20-Kilometer-Strecke wie ein Maßstab, der den Teilchen entgegenfliegt. Die Flugstrecke wird dadurch anscheinend verkürzt wahrgenommen und beträgt nur noch 1250 Meter. Die Wahrscheinlichkeit, den so verkürzten Weg zur Erde ohne Zerfall zu passieren, ist wieder 15 Prozent. In beiden Bezugssystemen erhalten wir also die gleiche physikalische Aussage.
Zwillingsparadoxon
Trotz dieser Symmetrie zwischen den beiden Inertialsystemen taucht ein ernsthaftes Problem auf. Um dies zu erkennen, vergleichen wir eine Gruppe 1 von Myonen, die im Laborsystem ruhen, mit einer Gruppe 2 von schnell bewegten Myonen. Vom Laborsystem aus gesehen gehen die Uhren im bewegten System langsamer – die Myonen der Gruppe 2 sollten also länger „leben“ als die Myonen der Gruppe 1. Vom mitbewegten System aus gesehen ist es gerade umgekehrt: Jetzt bewegt sich das Laborsystem mit hoher Geschwindigkeit, seine Uhren sind entsprechend verlangsamt und folglich sollten die Myonen der Gruppe 1 länger leben als die Myonen der Gruppe 2. Diese beiden, in der Relativitätstheorie vollkommen legitimen Betrachtungsweisen, führen offenbar zu widersprüchlichen Aussagen.
Was ist nun richtig? Das ist gar nicht so leicht zu sagen, denn die beiden Teilchengruppen fliegen immer weiter voneinander weg, und es lässt sich nicht mehr nachprüfen, welche tatsächlich eher zerfallen, die im Labor bewegten oder die im Labor ruhenden Myonen. Dies ist das berühmte „Zwillingsparadoxon“. Es gibt jedoch ein Experiment, mit dem eine Entscheidung möglich ist, und dieses beruht darauf, dass die Zeitdehnung auch in beschleunigten Koordinatensystemen auftritt. Am Brookhaven National Laboratory im US-Bundesstaat New York und am Forschungszentrum CERN bei Genf wurden kreisförmige Speicherringe für hochenergetische Myonen gebaut worden. In einem Speicherring kehren die Teilchen immer wieder zu ihrem Ausgangspunkt zurück, und man kann ohne Schwierigkeiten die Lebensdauern der ruhenden und der schnell bewegten Teilchen vergleichen.
In ihrem Experiment verglichen die Wissenschaftler zehntausend ruhende Teilchen im Labor mit zehntausend schnell bewegten Teilchen im Speicherring. Die Messung zeigte, dass nach zwanzig Mikrosekunden kein einziges ruhendes Myon mehr vorhanden ist, aber noch 8600 bewegte Myonen. Das Einsteinsche Zwillingsparadoxon ist hier in spektakulärer Weise realisiert: Die meisten schnell bewegten Myonen existieren noch, während die ruhenden Teilchen schon alle zerfallen sind. Diese eindeutige Aussage zugunsten der schnellen Myonen resultiert daraus, dass die beiden Bezugssysteme in diesem Versuch nicht gleichberechtigt sind: Das Laborsystem ist ein Inertialsystem, das mitbewegte System im Speicherring hingegen ähnelt einem Karussell und stellt ein beschleunigtes System dar. Aus diesem Grund ist zwischen den beiden Systemen keine Symmetrie mehr vorhanden.
Relativitätstheorie und Teilchenbeschleuniger
Eine andere und sehr wichtige Konsequenz der Relativitätstheorie ist die relativistische Massenzunahme: Bei einem schnell bewegten Teilchen ist die Masse um den Lorentzfaktor größer als bei dem ruhenden Teilchen. Nähert man sich der Lichtgeschwindigkeit an, so wächst dieser Faktor und damit auch die „bewegte Masse“ ins Unendliche. Dies ist der Grund dafür, dass Teilchen mit einer von Null verschiedenen Ruhemasse die Lichtgeschwindigkeit niemals exakt erreichen können, man bräuchte unendlich viel Energie dafür. Die Geschwindigkeit massiver Teilchen ist also stets kleiner als c. Anders ist dies bei den Lichtquanten, auch Photonen genannt; sie haben keine Ruhemasse und bewegen sich stets mit Lichtgeschwindigkeit.
Die relativistische Massenzunahme von Elektronen und Protonen sowie die Tatsache, dass ihre Maximalgeschwindigkeit die Lichtgeschwindigkeit nie übersteigt, spielen eine herausragende Rolle in Kreisbeschleunigern. Elektronen oder Protonen werden hier in kreisförmigen Tunneln beschleunigt und durch Magnete auf der Bahn gehalten. Die Stärke der Magnetfelder muss dabei genau auf die bewegte Masse der beschleunigten Teilchen abgestimmt sein, um diese auf der vorhergesehenen Kreisbahn zu halten.
Beim Protonenbeschleuniger HERA in Hamburg wurden die Teilchen mit einer Energie von 40 Gigaelektronenvolt (GeV) eingeschossen und auf 920 GeV beschleunigt. (Um die Energie von 920 GeV zu erreichen, müssen die Protonen eine riesige Beschleunigungsspannung von insgesamt 920 Milliarden Volt durchlaufen. Eine Hochspannungsüberlandleitung hat weit weniger als eine Million Volt). Bereits beim Einschuss haben die Protonen eine Geschwindigkeit von 99,97 Prozent der Lichtgeschwindigkeit, bei der Maximalenergie sind es 99,99995 Prozent. Berechnet man die benötigten Magnetfelder einerseits mit klassischen und andererseits mit relativistischen Gleichungen, ist der Unterschied enorm: Aus der nichtrelativistischen Formel ergibt sich ein Feld von 0,05 Tesla. Gemäß der relativistischen Gleichung muss das Feld in den supraleitenden Magneten dagegen einen Wert von 0,23 Tesla bei 40 GeV und 5,2 Tesla bei 920 GeV besitzen. Genau diese Feldwerte wurden beim Betrieb von HERA eingestellt, und die Maschine funktionierte in der Tat einwandfrei. Obwohl also die Geschwindigkeit der Protonen zwischen 40 und 920 GeV nur noch unwesentlich zunimmt, muss das Magnetfeld um das 23-fache ansteigen. Dieses Anwachsen ist genau proportional zum Anwachsen der bewegten Masse.
Das Beispiel HERA zeigt, dass der Begriff Beschleuniger bei relativistischen Energien eigentlich unangebracht ist. Die Geschwindigkeit ändert sich im HERA-Ring kaum noch, die Beschleunigung ist vernachlässigbar klein. Stattdessen wird die Energiezufuhr primär genutzt, um die bewegte Masse zu vergrößern. Man sollte diese Maschinen also eigentlich „Massenerhöher“ nennen, aber der Name Beschleuniger (engl. accelerator, franz. accelerateur, niederl. versneller) hat sich so sehr eingebürgert, dass er wohl nicht mehr zu ändern ist.
Lorentztransformation
Jedes Objekt – ob Mensch, Auto oder Elementarteilchen – befindet sich in seinem eigenen Bezugssystem, dass sich durch ein Koordinatensystem charakterisieren lässt. Betrachten wir wieder die Frau auf dem Rollsteig, der sich relativ zum ruhenden Boden bewegt. Im Rollsteig sei das Koordinatensystem \( (x\!^*, y\!^*, z\!^*) \) verankert, das sich mit konstanter Geschwindigkeit parallel zur x-Achse des Laborsystems \( (x, y, z) \), die in diesem Fall die ruhende Flughafenhalle ist, bewegt (siehe Grafik Inertialsystem). Die Position der Frau auf dem Rollband lässt sich mithilfe beider Koordinatensysteme eindeutig beschreiben. Wechselt man zwischen den beiden Bezugssystemen, müssen auch die Koordinaten transformiert werden.
Der wesentliche Punkt ist, dass auch die Zeit transformiert werden muss. Genau das leistet die sogenannte Lorentztransformation, benannt nach dem holländischen Physiker Hendrik Antoon Lorentz:
$$ t = \gamma \; \left( t\!^* + \frac{v}{c^2}x\!^* \right) $$
$$ x = \gamma \; \left(x\!^* + v t\!^* \right) $$
$$ y = y\!^* $$
$$ z = z\!^* $$
Hierbei sind v die Relativgeschwindigkeit der beiden Bezugssysteme und c die Lichtgeschwindigkeit. \( t \) und \( t\!^* \) stehen für die Zeit, während \( \gamma \) den Lorentzfaktor darstellt. Bemerkenswert an der Lorentztransformation ist, dass nur die Zeit und die zur Bewegungsrichtung parallele Koordinate (hier \( x \) ) transformiert werden, während die dazu senkrechten Koordinaten (hier \( y \) und \( z \)) unverändert bleiben. Der Lorentzfaktor kann folgendermaßen beschrieben werden:
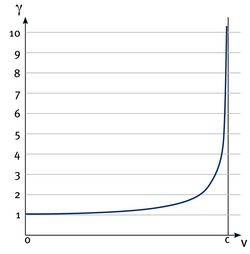
$$ \gamma = \frac{1}{ \sqrt{1-(v^2/c^2)} } $$
In relativ zueinander bewegten Koordinatensystemen gelten verschiedene Zeitskalen. Diese kühne und folgenreiche Annahme ist unvermeidlich, um zu gewährleisten, dass Licht in allen Bezugssystemen immer die gleiche Geschwindigkeit \( c \) hat. Für niedrige Geschwindigkeiten – \( v \) ist in diesem Fall viel kleiner als \( c \) – wird der Lorentzfaktor ungefähr 1 (siehe Grafik Lorentzfaktor). Aus den Formeln der Lorentztransformation folgt dann \( t = t\!^* \), das heißt, die Zeitskalen werden identisch und es gibt eine absolute Zeit.
Addition von Geschwindigkeiten
Ein Laufband in einer Flughafenhalle besitze die Geschwindigkeit \( v \), während sich eine Person darauf mit der Geschwindigkeit \( u\!^* \) relativ zum Laufband fortbewegt (siehe Grafik Inertialsystem). Die Geschwindigkeit der Person relativ zum Fußboden der Flughafenhalle ist dann durch folgende, relativistisch korrekte, Formel gegeben:
$$ u = \frac{ v + u\!^* }{1 + v u\!^* / c^2}. $$
Die Geschwindigkeiten \( v \) und \( u\!^* \) von Laufband und Fußgänger betragen wenige Meter pro Sekunde und sind damit deutlich kleiner als die Lichtgeschwindigkeit \( c \). Daher ist der Nenner in der obigen Formel praktisch gleich 1, und der Ausdruck lässt sich zu \( u = v + u\!^* \) vereinfachen. Die Geschwindigkeiten werden also wie gewohnt addiert.
Anders verhält es sich bei einem Lichtblitz, der sich mit der Geschwindigkeit \( u\!^* = c \) relativ zum Laufband ausbreitet: Anwenden der relativistischen Formel ergibt hier \( u = c \). Das Licht besitzt also auch relativ zum Fußboden der Flughafenhalle genau die Geschwindigkeit \( c \). Wie schnell oder langsam sich das Laufband bewegt, ist dabei völlig egal.
Lichtgeschwindigkeit und die Definition des Meters
Seit mehr als 200 Jahren benutzen Menschen die Längeneinheit Meter. Aber wie lang ist eigentlich ein Meter? Diese Frage ist alles andere als trivial und so änderte sich die Definition des Meters im Lauf der Zeit schon mehrfach. Von Pendellängen, über Bruchteile von Längenkreisen auf der Erdoberfläche bis hin zum in Edelmetall gegossenen Ur-Meter. Seit 1983 ist die Einheit nun als die Länge der Strecke definiert, die Licht in einer Zeitdauer von 1/299.792.458 Sekunden im luftleeren Raum zurücklegt. Die aktuelle Meterdefinition gibt damit einen exakten Zahlenwert für die Lichtgeschwindigkeit vor; die Konstante c ist dadurch genau festgelegt auf 299.792.458 Meter pro Sekunde.
Quelle: https://www.weltderphysik.de/thema/albert-einstein-und-die-relativitaetstheorie/spezielle-relativitaetstheorie/