Kolloidale Kristalle in eingeschränkter Geometrie

Kolloide, also fein verteilte Schwebstoffe in einem Trägermedium, ordnen sich normalerweise zu hoch symmetrischen Strukturen an, die eine maximale Raumfüllung anstreben. Äußere Einschränkungen der Geometrie zwingen Kolloide zuweilen aber dazu, von ihrer bevorzugten Kristallstruktur abzuweichen.

Während Orangen gestapelt eine raumfüllende Pyramidenstruktur einnehmen, beobachtet man zuweilen auch stabile quadratische Anordnungen, wenn die Orangen in Kisten liegen. Die Beschränkung der Geometrie ändert also die Struktur. Ähnliches lässt sich auch bei Kolloiden beobachten, wenn sich diese nicht etwa in einem großen Glasbehälter befinden (siehe Artikel Kolloidale Kristalle und Kugelpackungen), sondern auf engstem Raum.

Strukturbildung bei Kolloiden

Strukturbildung bei Kolloiden

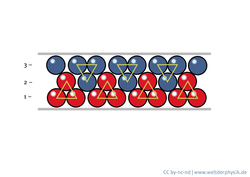
Dazu nehmen wir an, dass die kolloidalen Kugeln so zwischen zwei Platten eingesperrt werden, dass nur genau eine einzige Lage Kugeln hineinpasst. Es wird sich ein hoch symmetrisches zweidimensionales Dreiecksgitter ergeben. Erhöht man den Abstand der Platten, entsteht zunächst einmal viel „Luft“. Irgendwann aber passen genau zwei Lagen der Kolloide in den verfügbaren Platz, dann drei – entweder in ABA- oder ABC-Stapelung.

Dass das tatsächlich so ist, konnten Forscher in den 1980er-Jahren erstmals nachweisen. Um die trianguläre Struktur sichtbar zu machen, nutzt man die Tatsache, dass die verschiedenen Stapelungen Licht unterschiedlich beugen. Im Mikroskop erkennt man dieses unterschiedliche Beugungsverhalten dann durch unterschiedliche Färbungen. Schaltet man in den Strahlengang eines Mikroskops zusätzlich eine weitere Linse, kann man sogar die Beugungsmuster direkt sichtbar machen. In diesen Beugungsmustern ist die sechszahlige Symmetrie besonders schön zu erkennen, die auf der entsprechenden Symmetrie des Kolloidkristalls beruht.

Effizient packen unter Einschränkung

Was aber passiert bei Abständen, die nicht genau diesen bestimmten Höhen entsprechen, das heißt, bei Abständen, die nicht die bevorzugte dreilagige Stapelung und damit die maximale Raumfüllung erlauben? Die Kolloide sind dann gezwungen, andere Wege zu finden, um sich anzuordnen. So gestattet beispielsweise eine Stapelung mit quadratischer Symmetrie andere Höhen als die hexagonale Symmetrie das zulassen würde. Hier sitzen die Partikel der oberen Lage dann in tieferen Zwickeln, so dass kleinere Gesamthöhen erreicht werden. Die unvermeidlich auftretende Platzverschwendung, die mit der quadratischen Stapelung einhergeht, ist dabei gar nicht so groß.

Prismen mit quadratischer Symmetrie

Die maximale Packungsdichte nimmt rasch mit der Anzahl an Lagen zu: Bei zwei quadratischen Lagen liegt sie bei 61 Prozent, bei drei Lagen bei 65 Prozent und bei fast 68 Prozent für vier Lagen. Sie kommt bereits bei zehn Lagen dem Keplerschen Idealwert von 74 Prozent sehr nahe. In jedem Fall ist bei diesen Höhen das freie Volumen viel kleiner als bei der gleichen Lagenzahl in Dreiecksanordnung.

Eine weitere Möglichkeit des Platzsparens besteht in der sogenannten Verkippung einer Stapelung. So kann zum Beispiel eine ABA-Stapelung senkrecht stehen. Im Lichtmikroskop sieht man dann ein charakteristisches Streifenmuster, in der elektronenmikroskopischen Aufnahme der Schnittkante die senkrecht stehenden Lagen. Alle diese Strukturen haben immer noch dieselbe hohe Symmetrie wie die Grundstruktur – man kann sie sich als dünne Ausschnitte aus dem ursprünglichen Kristall denken. Jede Symmetrie entspricht dann jeweils einer bestimmten Schnittrichtung, allerdings kann sich bei der geometrischen Operation des „Schneidens“ die globale Symmetrie verringern.

Flexible Symmetrieeinheiten

Grafische Darstelung: Packungsproblem

Es gibt aber noch einen weiteren Trick, um effizient zu packen, ohne die Symmetrie allzu sehr zu vermindern. Bei bestimmten Höhen bevorzugt das kolloidale Kugelsystem nämlich ein Aufbrechen in dichtest gepackte Untereinheiten, die dann ihrerseits gestapelt werden. Unter Umständen ergibt sich damit eine überaus flexible Anpassung an wechselnde Zellhöhen. Man kann sich etwa eine ABC-gestapelte Dreifachlage auch aus prismatischen Blöcken, ähnlich denen der Toblerone-Schokolade, zusammengesetzt denken. Auch unter sehr engen Verhältnissen in einem Schlitz lassen sich diese gut gegeneinander verschieben, wobei sie gegenseitig „auf Rille“ abgleiten können, sobald der Schlitz höher gemacht wird. Schließlich rasten die Prismen in einer vierlagigen Struktur wieder ein.

Auf diese Weise wird nur noch sehr wenig Platz verschwendet und das klappt auch mit Prismen, die eine quadratische Basis haben. Dort werden einzelne dicht gepackte Teile einer Stapelung quadratischer Lagen gegeneinander verschoben. Mit etwas Geduld, etwas Kleber und einigen Dutzend Murmeln lässt sich das sogar leicht im Modell nachbauen. Insbesondere bei großen Plattenabständen findet man dabei auch deutlich kompliziertere Unterteilungen in einzelne Blöcke. Jedes Mal bleibt innerhalb dieser Blöcke die ursprünglich dichteste Packung – also kubisch-raumzentriert oder hexagonal – erhalten, aber es treten neben Prismen auch Platten, Quader oder einfache Stangen auf.

Konflikt zwischen globaler und lokaler Symmetrie

Wechselspiel von Symmetrie und beschränktem Platz

Auf diese Weise vermindert die Natur also die globale Symmetrie, kann aber gleichzeitig eine hohe lokale Symmetrie erhalten und die Packung optimieren. Dies kann unter Umständen auch bei Volumenproben notwendig sein: Beginnt nach einem Aufschütteln der Probe nämlich die Kristallisation, so entstehen die Kristallite über Keimungsprozesse an völlig zufälligen Stellen und mit zufälligen Orientierungen. Wenn diese Keime zu großen Kristallen herangewachsen sind, stoßen sie zusammen. Dabei treten häufig mechanische Verspannungen auf, da die Kristallkanten nicht optimal zusammenpassen. Um die mechanische Energie zu verringern, hilft sich der Kristall dann gewissermaßen selbst, indem ganze Blöcke von Ebenen gegeneinander abgleiten. In der polarisationsmikroskopischen Aufnahme sieht man dann in den Kristallen streifenartige Zonen unterschiedlicher Farbe. Das Wechselspiel zwischen Symmetrie und beschränktem Platz zeigt sich so von seiner reizvollsten Seite.